sympy
A computer algebra system written in pure Python
What's the (best) way to solve a pair of non linear equations using Python. (Numpy, Scipy or Sympy)
eg:
A code snippet which solves the above pair will be great
Source: (StackOverflow)
I'm trying to represent the ring;

where theta is the root of a monic irreducible polynomial f with integer coefficients of degree d.
This ring is a subring of the algebraic integers, which itself is a subring of the field;

I can represent this field with sympy's AlgebraicField class
Q_theta = sympy.polys.domains.AlgebraicField(QQ,theta)
Is there a way to represent the above integer subring in a similar way?
Source: (StackOverflow)
When plotting a graph with a discontinuity/asymptote/singularity/whatever, is there any automatic way to prevent Matplotlib from 'joining the dots' across the 'break'? (please see code/image below).
I read that Sage has a [detect_poles] facility that looked good, but I really want it to work with Matplotlib.
import matplotlib.pyplot as plt
import numpy as np
from sympy import sympify, lambdify
from sympy.abc import x
fig = plt.figure(1)
ax = fig.add_subplot(111)
# set up axis
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
# setup x and y ranges and precision
xx = np.arange(-0.5,5.5,0.01)
# draw my curve
myfunction=sympify(1/(x-2))
mylambdifiedfunction=lambdify(x,myfunction,'numpy')
ax.plot(xx, mylambdifiedfunction(xx),zorder=100,linewidth=3,color='red')
#set bounds
ax.set_xbound(-1,6)
ax.set_ybound(-4,4)
plt.show()
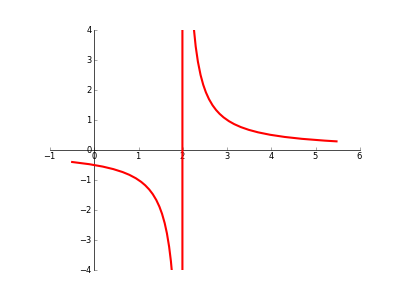
Source: (StackOverflow)
I'm experimenting with sympy and I've hit upon an issue I can't work out.
Using scipy I can write an expression and evaluate it for an array of x values as follows:
import scipy
xvals = scipy.arange(-100,100,0.1)
f = lambda x: x**2
f(xvals)
Using sympy I can write the same expression as follows:
import sympy
x = sympy.symbols('x')
g = x**2
I can evaluate this expression for a single value by doing the following:
g.evalf(subs={x:10})
However I can't work out how to evaluate it for an array of x values, like I did with scipy. How would I do this?
Source: (StackOverflow)
I solved a quadratic equation using sympy:
import sympy as sp
q,qm,k,c0,c,vt,vm = sp.symbols('q qm k c0 c vt vm')
c = ( c0 * vt - q * vm) / vt
eq1 = sp.Eq(qm * k * c / (1 + k * c) ,q)
q_solve = sp.solve(eq1,q)
Based on some testing I figured out that only q_solve[0] makes physical sense. Will sympy always put (b - sqrt(b**2 - 4*a*c))/2a in the first place ? I guess, it might change with an upgrade ?
Source: (StackOverflow)
I would like to plot implicit equations (of the form f(x, y)=g(x, y) eg. X^y=y^x) in Matplotlib. Is this possible?
Source: (StackOverflow)
I need a calculate below expression using sympy in python?
exp = '(a+b)*40-(c-a)/0.5'
In a=6, b=5, c=2 this case how to calculate expression using sympy in python? Please help me.
Source: (StackOverflow)
What happens internally when I press Enter?
My motivation for asking, besides plain curiosity, is to figure out what happens when you
from sympy import *
and enter an expression. How does it go from Enter to calling
__sympifyit_wrapper(a,b)
in sympy.core.decorators? (That's the first place winpdb took me when I tried inspecting an evaluation.) I would guess that there is some built-in eval function that gets called normally, and is overridden when you import sympy?
Source: (StackOverflow)
I'm trying to nice print some divisions with Sympy but I noticed it didn't display aligned.
import sympy
sympy.init_printing(use_unicode=True)
sympy.pprint(sympy.Mul(-1, sympy.Pow(-5, -1, evaluate=False), evaluate=False))
# Output:
# -1
# ───
# -5 # Note that "-5" is displayed slightly more on the right than "-1".
Reason/fix for this?
EDIT: I did a lot of reverse-engineering using inspect.getsource and inspect.getsourcefile but it didn't really help out in the end.
Pretty Printing in Sympy seems to be relying on the Prettyprinter by Jurjen Bos.
import sympy
from sympy.printing.pretty.stringpict import *
sympy.init_printing(use_unicode=True)
prettyForm("-1")/prettyForm("-5")
# Displays:
# -1
# --
# -5
So it does display aligned, but I can't get it to use unicode.
The PrettyPrinter is called from the file sympy/printing/pretty/pretty.py in the method PrettyPrinter._print_Mul which simply return prettyForm.__mul__(*a)/prettyForm.__mul__(*b) with, I thought, a and b simply being ['-1'] and ['-5'] but it wouldn't work.
Source: (StackOverflow)
SymPy is a great tool for doing units conversions in Python:
>>> from sympy.physics import units
>>> 12. * units.inch / units.m
0.304800000000000
You can easily roll your own:
>>> units.BTU = 1055.05585 * units.J
>>> units.BTU
1055.05585*m**2*kg/s**2
However, I cannot implement this into my application unless I can convert degrees C (absolute) to K to degrees F to degrees R, or any combo thereof.
I thought maybe something like this would work:
units.degC = <<somefunc of units.K>>
But clearly that is the wrong path to go down. Any suggestions for cleanly implementing "offset"-type units conversions in SymPy?
Note: I'm open to trying other units conversion modules, but don't know of any besides Unum, and found it to be cumbersome.
Edit: OK, it is now clear that what I want to do is first determine if the two quantities to be compared are in the same coordinate system. (like time units reference to different epochs or time zones or dB to straight amplitude), make the appropriate transformation, then make the conversion. Are there any general coordinate system management tools? That would be great.
I would make the assumption that °F and °C always refer to Δ°F Δ°C within an expression but refer to absolute when standing alone. I was just wondering if there was a way to make units.degF a function and slap a decorator property() on it to deal with those two conditions.
But for now, I'll set units.C == units.K and try to make it very clear in the documentation to use functions convertCtoK(...) and convertFtoR(...) when dealing with absolute units. (Just kidding. No I won't.)
Source: (StackOverflow)
I'm trying to use [SymPy][1] to substitute multiple terms in an expression at the same time. I tried the [subs function][2] with a dictionary as parameter, but found out that it substitutes sequentially.
In : a.subs({a:b, b:c})
Out: c
The problem is the first substitution resulted in a term that can be substituted by the second substitution, but it should not (for my cause).
Any idea on how to perform the substitutions simultaneously, without them interfering with each other?
Edit:
This is a real example
In [1]: I_x, I_y, I_z = Symbol("I_x"), Symbol("I_y"), Symbol("I_z")
In [2]: S_x, S_y, S_z = Symbol("S_x"), Symbol("S_y"), Symbol("S_z")
In [3]: J_is = Symbol("J_IS")
In [4]: t = Symbol("t")
In [5]: substitutions = (
(2 * I_x * S_z, 2 * I_x * S_z * cos(2 * pi * J_is * t) + I_y * sin(2 * pi * J_is * t)),
(I_x, I_x * cos(2 * pi * J_is * t) + 2 * I_x * S_z * sin(2 * pi * J_is * t)),
(I_y, I_y * cos(2 * pi * J_is * t) - 2 * I_x * S_z * sin(2 * pi * J_is * t))
)
In [6]: (2 * I_x * S_z).subs(substitutions)
Out[7]: (I_y*cos(2*pi*J_IS*t) - 2*I_x*S_z*sin(2*pi*J_IS*t))*sin(2*pi*J_IS*t) + 2*S_z*(I_x*cos(2*pi*J_IS*t) + 2*I_x*S_z*sin(2*pi*J_IS*t))*cos(2*pi*J_IS*t)
Only the appropriate substitution should happen, in this case only the first one. So the expected output should be the following:
In [6]: (2 * I_x * S_z).subs(substitutions)
Out[7]: I_y*sin(2*pi*J_IS*t) + 2*I_x*S_z*cos(2*pi*J_IS*t)
Source: (StackOverflow)
I want to parse LaTeX formulas and directly use them as SymPy expressions. In other words, what I need is something similar to sympify:
from sympy import sympify
f = sympify('x^2 + sin(y) + 1/2')
print f
but that can take LaTeX expressions (strings) as input, for example:
f = latex_sympify('\frac{x}{1+x}')
Given that sympify is able to convert a string with a regular mathematical expression into a SymPy object, if there is anything that can convert LaTeX into a regular mathematical expression, I guess that would do the trick---but I would prefer to do everything within Python.
Any suggestions will be much appreciated.
Source: (StackOverflow)
I wrote the following program in Python 2 to do Newton's method computations for my math problem set, and while it works perfectly, for reasons unbeknownst to me, when I initially load it in ipython with %run -i NewtonsMethodMultivariate.py, the Python 3 division is not imported. I know this because after I load my Python program, entering x**(3/4) gives "1". After manually importing the new division, then x**(3/4) remains x**(3/4), as expected. Why is this?
# coding: utf-8
from __future__ import division
from sympy import symbols, Matrix, zeros
x, y = symbols('x y')
X = Matrix([[x],[y]])
tol = 1e-3
def roots(h,a):
def F(s):
return h.subs({x: s[0,0], y: s[1,0]})
def D(s):
return h.jacobian(X).subs({x: s[0,0], y: s[1,0]})
if F(a) == zeros((2,1)):
return a
else:
while (F(a)).norm() > tol:
a = a - ((D(a))**(-1))*F(a)
print a.evalf(10)
I would use Python 3 to avoid this issue, but my Linux distribution only ships SymPy for Python 2. Thanks to the help anyone can provide.
Also, in case anyone was wondering, I haven't yet generalized this script for nxn Jacobians, and only had to deal with 2x2 in my problem set. Additionally, I'm slicing the 2x2 zero matrix instead of using the command zeros(2,1) because SymPy 0.7.1, installed on my machine, complains that "zeros() takes exactly one argument", though the wiki suggests otherwise. Maybe this command is only for the git version. (Thanks eryksun for correcting my notation, which fixed the issue with the zeros function.)
Source: (StackOverflow)
I'm solving the integral numerically using python:

where a(x) can take on any value; positive, negative, inside or outside the the [-1;1] and eta is an infinitesimal positive quantity. There is a second outer integral of which changes the value of a(x)
I'm trying to solve this using the Sokhotski–Plemelj theorem:

However this involves determining the principle value, which I can't find any method to in python. I know it's implemented in Matlab, but does anyone know of either a library or some other way of the determining the principal value in python (if a principle value exists)?
Source: (StackOverflow)
I have just started with using IPython Notebook and have been fascinated by its power. I have been using a few examples available on the net to get started with. I was following this tutorial: http://nbviewer.ipython.org/url/finiterank.com/cuadernos/suavesylocas.ipynb but the maths output is not getting rendered as expected. Below is the my code and the output:
In [30]:
%load_ext sympyprinting
%pylab inline
from __future__ import division
import sympy as sym
from sympy import *
init_printing()
x,y,z=symbols("x y z")
k,m,n=symbols("k m n", integer=True)
The sympyprinting extension is already loaded. To reload it, use:
%reload_ext sympyprinting
Welcome to pylab, a matplotlib-based Python environment [backend: module://IPython.kernel.zmq.pylab.backend_inline].
For more information, type 'help(pylab)'.
In [31]:
t = sin(2*pi*x*(k**2))/ (4*(pi**2)*(k**5)) + (x**2) / (2*k)
t
Out[31]:
2 ⎛ 2 ⎞
x sin⎝2⋅π⋅k ⋅x⎠
─── + ─────────────
2⋅k 2 5
4⋅π ⋅k
I have tried other examples also, and they are also not getting rendered properly. Where am I going wrong?
Source: (StackOverflow)